Consistent hashing is a strategy most notably used by distributed databases for determining to which slot a key belongs. Its main advantage is that if a new slot needs to be added, only K/n objects need to be moved (K=number of all keys, n=the number of slots). And this means adding and removing slots is relatively inexpensive.
In Practice
Let’s say you have implemented a very successful online telephone book. Your users enter a person’s name and get their telephone number. You already have millions of person-phone mappings and more are added every day. Your DB server will soon not be able to handle the number of requests, thus you decided to partition the database.
-
First, you have to choose a
key.Read and write requests to the DB will always be done for a specific person’s name. This means your key should be calculated from a person’s name.
key = some_hash_function(person.name)When choosing a hash function, it is good to choose one, which distributes hashes uniformly.
Let’s say that our
some_hash_functioncreates integer values between 0 and 1023. -
Next, you need to choose the number of partitions or
slots.Let’s say we will have 4 partitions.
4 was chosen completely at random. Considering our example it would have been enough to split the DB in half instead of into quarters, but it is easier to illustrate consistent hashing with more slots.
-
Now you need to map the
slotsinto the same hash-space as thekeys.We need to give each of our 4 partitions a hash value and this hash value must also be between 0 and 1023 just like the results of
some_hash_function.We can use any method to define the hashes of our 4 partitions. Let’s say we have chosen the following values:
Partition0: 100 Partition1: 400 Partition2: 700 Partition3: 900 -
In the last step, we define the way the
keysmap toslots.Here is what we have until now:
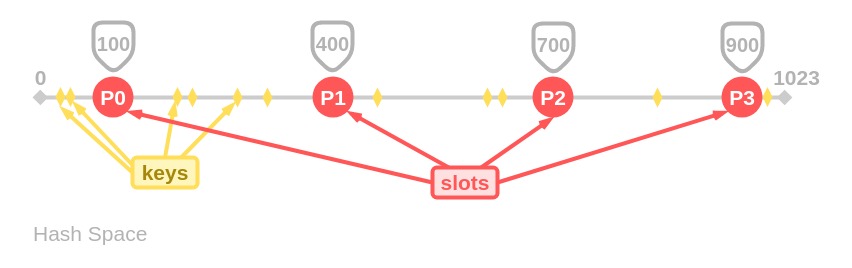
Our hash space extends from 0 to 1023. All the
keys(=person’s names) and all theslots(=DB partitions) have their position in the same hash space.To avoid having to deal with the start and the end, the hash space is usually drawn as a circle. Like this:
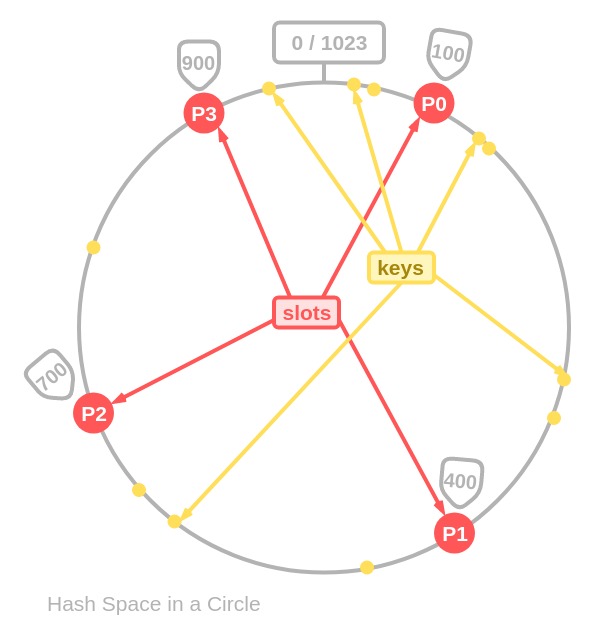
Every
keybelongs to the firstslotto the right on the circle. In our case all keys 0 - 100 belong to Partition0, 101 - 400 to Partition1, 401 - 700 to Partition2, 701 - 900 to Partition3. And the keys, which are bigger than 900, where do they belong? Also to the nextsloton the circle, which is Partiotion0.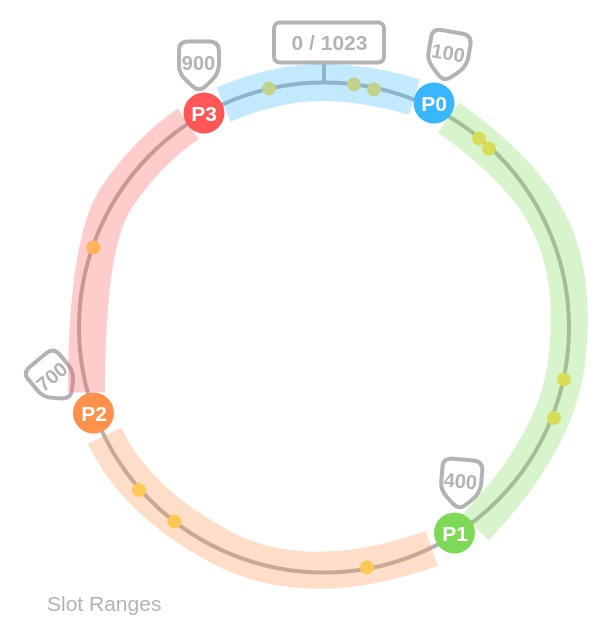
What have we gained
Adding and removing of servers is relatively inexpensive.
If we add a server at roughly hash 250, then only the 2 keys after P0 and before 250 need to be moved to the new server.
If we remove the server P3, then only its 1 key needs to be moved to P0.
Moving of keys is always done to the new server or from a removed server, never between existing servers.
We are also not storing any information in any kind of a global directory. Our partitions are completely independent of each other.
Gotchas
How to choose the hash function
Your hash function should distribute keys evenly over the whole hash space. But it should also be fast. There is no need to take a cryptographic hash function, as these are usually on the slower side.
Wikipedia holds a list of hash functions
How to remediate an uneven distribution of keys
In the real world, the distribution of keys and slots is often not even with most keys stored in just a few slots, leaving other slots mostly empty. This is usually addressed with virtual slots. Each physical server is responsible for several virtual servers.
Each physical server gets multiple slots on the ring, these slots do not have to be together. This has 2 advantages:
- when a physical server fails, its
keysare redistributed to many otherslots, not just to its next neighbour - with many
slots, the number ofkeysperslotgoes down and the distribution ofkeysamongslotsbecomes more even
How to remediate some physical servers having better performance than others
This problem as well is solved with virtual servers. The number of virtual slots for each physical server is determined based on the performance of the physical server.